원자 스펙트럼 계열(Atomic spectral series) 연구의역사에 대한 에세이 : s, p, d, f 명칭의 기원과 의미 (2025년 5월호)

한상준 | 한국과학영재학교, 화학교사 sangjoon.hahn@gmail.com

서 론 

19세기 후반부터 20세기 초까지, 수소와 알칼리 금속 원자의 방출 스펙트럼은 원자 내부 구조에 대한 실마리를 제공하는 중요한 연구 대상이었다. 특히 수소와 알칼리 금속 원자의 스펙트럼은 계열을 이루며 반복적인 패턴을 보였고, 이는 원자 내부에 어떤 정해진 구조가 존재한다는 강력한 단서를 제공했다. 1885년, 발머(Balmer)는 수소 원자의 가시광선 영역 스펙트럼을 간단한 수학식으로 표현했고, 이를 일반화한 리드버그(Rydberg)는 다양한 원소의 스펙트럼선들이 공통된 수학적 구조를 가진다는 사실을 밝혀냈다. 1908년, 리츠(Ritz)는 여러 스펙트럼선들이 서로의 파수 조합으로 표현된다는 조합 원리를 제안함으로써, 스펙트럼선들이 에너지 준위 간 전이에 해당한다는 개념을 이론적으로 뒷받침했다. 이러한 경험적 법칙들은 단순한 선 배열의 규칙을 넘어서, 원자 내부에 양자화된 에너지 준위가 존재한다는 사실을 예고하고 있었다. 실제로 리츠의 조합 원리는 파셴(Paschen)에게 수소의 적외선 계열을 예측하고 발견하는 데 결정적인 이론적 도구가 되었다. 이러한 발견들은 전자 에너지가 불연속적인 값만을 가질 수 있다는 양자역학의 개념을 실험적으로 지지해 주었고, 이후 보어(Bohr)의 원자 모형과 슈뢰딩거 방정식에 기반한 현대 원자 이론의 출발점이 되었다. 본 에세이에서는 원자 스펙트럼 계열의 연구가 현대 물리학의 토대를 형성하는 데 어떠한 기여를 했는지 조명하고자 한다. 

본 론 

가. 19세기: 선 스펙트럼의 관찰과 초기 분류 

19세기 중반까지 과학자들은 프라운호퍼(Fraunhofer)가 발견한 태양 스펙트럼선 등 원소의 고유한 선 스펙트럼을 연구하고 있었지만, 선들의 모양(선폭과 선명도)에 따라 체계적으로 분류하지는 못하고 있었다. 1860년대 분젠(Bunsen)과 키르히호프(Kirchhoff)는 각 원소가 고유한 파장의 스펙트럼선을 낸다는 것을 보여주었고, 이후 여러 원소의 스펙트럼이 정밀 측정되었다. 그러던 중 1870년대에 영국의 조지 라이빙(George Liveing)과 제임스 듀어(James Dewar)가 알칼리 금속 등의 스펙트럼선을 체계적으로 측정하면서, 선들의 강도와 뚜렷함의 차이에 주목했다. 이들은 어떤 선들은 매우 뚜렷하고 가느다란 반면 다른 선들은 번진 듯 희미하거나 넓게 보인다는 것을 알아내고, 이러한 특징에 따라 스펙트럼선들을 묘사하기 시작했다. 특히 나트륨의 스펙트럼선을 조사하면서 한 줄씩 교대로 날카로운(sharp) 선과 퍼진(diffuse) 선이 반복되는 경향을 발견하고, 선들의 형태에 따라 “sharp”와 “diffuse”라는 용어를 처음 사용했다 . 1890년에는 흡수 스펙트럼에서 강하게 나타나는 선들을 principal series (주 계열)이라고 명명하였다. 

라이빙과 듀어는 이렇게 “principal”, “sharp”, “diffuse” 세 종류로 선들을 기술하였으며 동일한 유형의 선들이 일정한 묶음(군)을 이루는 경향이 있음을 보고했다. 

이렇게 하여 19세기 말까지 알칼리 금속 원소의 스펙트럼은 Principal (P), Sharp (S), Diffuse (D) 세 계열로 구분되어 불리게 되었다. [참고문헌 1 ]

나. 수소 원자 스펙트럼과 발머의 연구(1885) 

스위스의 수학자 요한 야코프 발머(Johann Balmer)는 1885년에 수소 원자의 가시광선 스펙트럼 선들의 파장을 설명하는 경험적 수식, 즉 발머 식(Balmer formula)을 발표하였다. 그는 수소 원자의 가시광선 방출선들이 일정한 수학적 패턴을 따른다는 사실을 발견했는데 그 식은 다음과 같은 형태를 띠었다. 

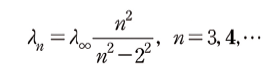
위 식에서 𝜆∞ 는 실험적으로 얻는 상수로 𝜆∞ = 363.56 𝑛𝑚 이었다. 

발머가 사용한 데이터는 𝐻𝛼, 𝐻𝛽, 𝐻𝛾, 𝐻𝛿 4개 선의 파장이었고 발머 식은 이 실험 데이터를 매우 잘 설명하였다. 발머는 수학 교사여서 분광학 분야에서 진행된 일을 잘 알지 못하였는데 사실 발머가 논문을 발표하기 5년 전인 1880년에 Huggins는 별빛과 성운의 스펙트럼을 측정하여 앞서 언급한 가시광선 대역의 4개의 선이외에도 자외선 대역에서 방출되는 수소 스펙트럼 선을 관찰한 데이터를 출판하였다. 발머는 추후 이 데이터를 뒤늦게 찾아보고 Huggins 측정한 이 데이터 들도 자신의 식으로 완벽히 설명할 수 있음을 알게 되었다.[표 1] 

다. 리드버그의 연구(1890) 

1885년 발머가 수소 원자의 가시광선 4개 선에 대한 발머식을 발표하여, 선들이 일정한 수학적 규칙(계열 공식)을 따른다는 것을 보여주자 , 다른 원소들 에서도 이러한 스펙트럼선 계열 공식을 찾으려는 연구가 활발해졌다. 1880년대 후반 독일의 카이저(Heinrich Kayser)와 룬게(Carl Runge), 스웨덴의 리드버그(Johannes Rydberg)는 알칼리 금속 원소들에서 보이는 세 개의 독립된 스펙트럼 계열을 구성하는 스펙트럼선들을 정량적으로 설명하는 식을 제안했다 . 

특히 리드버그는 그 당시까지 분석된 모든 알칼리 원소들의 스펙트럼에서, 서로 다른 파장을 갖는 선들이 어떤 정수 법칙을 따르고 있다며 각 계열의 선의 파수(wavenumber)의 위치 를 다음과 같은 리드버그 식의 형태로 표현하여 설명하였다.[참고문헌 2,3]

즉, 리드버그 식은 계열 수렴선이라고 하는 고정항(첫 번째 항)과 진행항(두 번째 항)으로 구성되고 진행항의 분모 부분에 양자결함 X라는 실수를 포함하고 있다. 

리드버그는 이 식을 Li 원자 스펙트럼의 Principal, Sharp, Diffuse 계열에 적용시켜 각 계열의 계열 수렴선 

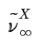
와 양자결함 X 를 구하여 다음과 같은 식을 얻을 수 있었다. 

한편 리드버그는 이 식으로부터 다음의 3가지 사실을 발견하였다.[참고문헌 1] 

1. Sharp 계열과 Diffuse 계열은 공통된 수렴선을 가진다. 

2. Sharp 계열과 Diffuse 계열의 공통 수렴선은 Principal 계열의 첫 번째 진행항 (n = 1)과 비슷하다. 

3. Principal 계열의 수렴선은 Sharp 계열의 첫 번째 진행항 (n = 1)과 비슷하다. 

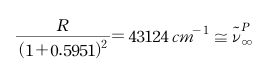
이 발견을 근거로 앞의 리드버그 식은 다음과 같이 표현할 수 있었다. 

즉, 알칼리 금속에서 측정되는 스펙트럼 선의 파수는 두 항(Term)의 차이로 표현 될 수 있었다. 

한편, 1896년 리드버그와 아서 슈스터(Arthur Schuster)는 알칼리 금속의 원자 스펙트럼으로 부터 다음의 사실을 발견하였다. 

“sharp 계열과 diffuse 계열의 공통 수렴 파수와 principal 계열의 수렴 주파수와의 차이는 principal 계열의 첫 번째 전이와 동일하다.” 

이를 수식으로 표현하면 다음과 같다. 

우리는 이 법칙을 리드버그–슈스터 법칙 (Rydberg–Schuster Law) 이라고 부른다. 우리는 리드버그가 발견한 3개의 사실과 리드버그–슈스터 법칙을 현대물리학의 관점에서 다음과 같이 설명할 수 있다. 즉, 양자역학에 의하면 전자는 불연속적인 여러 에너지 준위(오비탈)에 존재할 수 있으며 각 계열은 전자들이 특정한 에너지 준위들 사이에서 전이할 때 방출하거나 흡수하는 빛의 파장들이 일정한 규칙을 가지고 모여 있는 선들의 집합을 의미하고 리드버그 식에 등장하는 각 항은 오비탈 에너지 준위에 해당한다. 

Sharp 계열과 Diffuse 계열은 공통된 수렴선을 가지는 이유는 두 계열 모두 공통된 p 오비탈이 관여하고 있기 때문이다. 

Sharp 계열과 Diffuse 계열의 공통 수렴선이 Principal 계열의 첫 번째 진행항(n=1)과 비슷한 이유는 이들이 p 오비탈의 에너지 준위에 해당하기 때문이다. 

또한 Principal 계열의 수렴선은 Sharp 계열의 첫 번째 진행항(n = 1)과 비슷한 이유는 이 값이 s 오비탈의 에너지 준위에 해당하기 때문이다. 

리드버그–슈스터 법칙이 

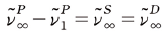
을 만족하는 이유도 [그림 2]의 알칼리 금속의 에너지 준위 다이어그램을 보면 쉽게 이해할 수 있다. 

한편 리드버그–슈스터 법칙(Rydberg–Schuster law)은 헬륨 원자의 단일항 상태(Singlet state)의 Principal 계열의 첫 번째 선을 예측하는데 중요한 역할을 하였다. 발머는 헬륨의 가시광선 및 자외선 스펙트럼선들에 대해서는 알고 있었지만, 적외선 영역에 대한 정보는 없었다. 그는 계열의 수렴선을 다음과 같이 찾았다: 

리드버그–슈스터 법칙(Rydberg–Schuster law)에 의하면 

이 적외선 영역인 2.057 μm에서 나타날 것이라고 예측했고, 파셴(Paschen)은 실제로 이를 2.058 μm에서 발견했다. 

리드버그–슈스터 법칙은 향후 이론 발전의 예고편이었다. 1908년에 제안된 리츠의 조합원리(Ritz Combination Principle)는 수소 원자의 근적외선 계열을 예측하고 발견한 데 위대한 업적을 이루었다.[참고문헌 4,5] 리츠는 발머가 이미 자신의 식을 다음 공식의 특수한 형태로 간주하고 있었다고 지적하면서 

형태의 계열 외에도

등과 같은 계열도 존재할 수 있다고 추정하였다. 그는 수소 원자의 스펙트럼은 일반적으로 다음의 형태를 가질 수 있다고 주장하였다.

즉, 이 원리에 의하면 모든 스펙트럼선은 두 항(Term)의 차로 표현될 수 있으며 

이 원리를 이용하면 아직 관측되지 않은 스펙트럼선의 파수를 예측할 수 있게 된다. 리츠는 수소 스펙트럼의 기존 선들(Balmer 계열 등)을 분석하여, 아직 발견되지 않은 선들도 Term 값 차이로 나타날 수 있다고 추론하고 새로운 선이 가시광선보다 더 긴 파장, 즉 적외선 대역에 존재할 수 있다고 예측하였다.[참고문헌 6,7] 파셴(Paschen)은 리츠(Ritz)의 계산을 바탕으로, 적외선 영역에서 수소 방전관의 스펙트럼을 측정했고, 실제로 새로운 계열 (n ≥ 4 → n = 3 전이)을 발견하였다. 그 계열은 나중에 Paschen 계열로 명명되었다. 그 이후로는, 스펙트럼 항(terms)이 물리적으로 실재하는 것임을 더 이상 부정할 수 없게 되었고, 비록 그것들을 이해하기는 어려웠다 하더라도, 실재하는 것으로 받아들여졌다. 

라. 20세기 초: 네번째 계열(F 계열)의 발견과 명칭 

세 계열 분류 체계는 알칼리 금속 등 여러 원소의 스펙트럼에 적용되었고, 이후 연구자들은 남아있는 스펙트럼선도 설명할 수 있는 추가 계열을 찾기 시작했다. 1907년 독일의 물리학자 아르노 베르크만(Arno Bergmann)은 알칼리 금속들의 적외선 영역 스펙트럼에서 새로운 계열의 선들을 발견하였는데, 이는 기존 세 계열로는 설명되지 않는 네번째 계열의 존재를 보여주었다 . 이 새로운 계열은 처음에는 “베르크만 계열”로 불렸으나, 1911년 윌리엄 힉스(William M. Hicks)가 이 계열을 가리켜 “기본(fundamental) 계열” 이라고 명명하였다 . 힉스는 이 새로운 계열이 마치 각 원소 스펙트럼의 기본이 되는 주파수에 해당한다고 생각하여 “Fundamental”이라는 용어를 붙였고, 기존의 Principal, Sharp, Diffuse 계열의 머리글자를 각각 P, S, D로 사용한 것처럼 이 계열에는 F라는 문자를 부여했다 . 그리하여 20세기 초까지 일반적으로 원자 스펙트럼에는 네 가지 유형의 선 계열, 즉 주요(P), 선명(S), 확산(D), 기본(F) 계열이 존재하는 것으로 정립되었다 . 한편 이러한 명칭은 엄밀한 과학적 정의 라기보다 경험적 관찰에 기반한 작명이었기 때문에, 가령 “sharp(선명)” 계열의 선도 경우에 따라서는 퍼져 보일 때가 있고 “fundamental(기본)” 계열의 선들은 오히려 스펙트럼에서 가장 희미하게 나타나는 등 이름과 현상의 매칭이 완벽하지는 않았다 . 그럼에도 이들 용어는 편의상 널리 쓰이게 되었고, 각 명칭은 해당 계열의 대표적 성격을 나타내는 것으로 받아들여졌다. 

결 론 

살펴본 바와 같이, 원자 스펙트럼의 계열 구조에 대한 연구는 단순한 선 배열의 관찰을 넘어서, 원자 내부에 존재하는 양자화된 에너지 준위를 간접적으로 드러내는 결정적인 실험적 증거를 제공했다. 발머의 경험적 수식은 수소 원자의 규칙적인 선 패턴을 처음으로 수학적으로 설명했고, 리드버그는 이를 일반화하여 다양한 원소의 스펙트럼에도 적용 가능한 공식을 제시했다. 리츠는 이 공식들을 바탕으로 모든 스펙트럼 선이 두 에너지 준위 사이의 차이로 설명될 수 있다는 조합 원리를 정립하였고, 이 원리는 이후 새로운 스펙트럼 계열(예: 파셴 계열)의 발견을 이끄는 강력한 이론적 도구로 작용하였다. 이처럼 스펙트럼의 계열성과 수학적 규칙성은 전자의 에너지가 불연속적인 값을 가진다는 사실을 뒷받침하였으며, 이는 보어의 원자모형, 양자역학, 오비탈 이론으로 이어지는 현대 원자 구조 이론의 기초를 이루는 데 핵심적인 역할을 하였다.[참고문헌 8] 따라서 스펙트럼 계열의 역사적 전개는 현대물리학의 발달을 이해하는 데 있어 하나의 중요한 이정표라고 할 수 있다.

참고문헌

1. Brand, J. C. D. Lines of Light; Gordon and Breach Publishers: 1995; 21. 

2. Rydberg, J. R. On the Structure of the Line Spectra of the Chemical Elements. Philos. Mag. 1980, 29, 331. 

3. Jammer, M. The Conceptual Development of Quantum Mechanics; McGraw-Hill: 1966; 65. 

4. Ritz, W. Zur Theorie der Serienspektren. Ann. Phys. 1903, 12(264). 

5. Ritz, W. Gesammelte Werke. Walter Ritz. Oeuvres; Gauthier-Villars: Paris, 1911. 

6. El’yashevich, M. A. Kembrovskaya, N. G.; Tomil’chik, L. M. Walter Ritz as a Theoretical Physicist and His Research on the Theory of Atomic Spectra. Phys. Usp. 1995, 38, 435. 

7. Hentschel, K. Walther Ritz’s Theoretical Work in Spectroscopy, Focussing on Series Formulae. Proc. Int. Conf. in Honor of Walther Ritz’s 100th Anniversary 2012, 129. 

8. Atkins, P.; de Paula, J. Physical Chemistry, 8th ed.; W.H. Freeman: 2006.

한상준 Sangjoon Hahn

• 서울대학교 화학과(물리화학전공), 박사(1992.3 – 1998.2. 지도교수: 김성근) 

• 한국과학영재학교 교사 (2005.3 - 현재)